Superlinearly Convergent Algorithms for Stochastic Time-Fractional Equations Driven by White Noise

Abstract

The numerical analysis of stochastic time-fractional equations exhibits a significantly low-order convergence rate since the limited regularity of model caused by the nonlocal operator and the presence of noise. In this work, we consider stochastic time-fractional equations driven by integrated white noise, where $^CD^α_t ψ(x, t),$ $0 < α < 2$ and $I^γ_t\dot{W} (x, t),$ $0 < γ < 1.$ We first establish the regularity of the mild solution. Then superlinear convergence rate

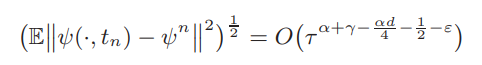
with sufficiently small ε term in the exponent is established based on the modified two-step backward difference formula methods. Here $d$ represents the spatial dimension, $ψ^n$ denotes the approximate solution at the $n$-th time step, and $\mathbb{E}$ is the expectation operator. Numerical experiments are performed to verify the theoretical results. To the best of our knowledge, this is the first topic on the superlinear convergence analysis for the stochastic time-fractional equations with integrated white noise.