Blowing Up Solutions to Slightly Sub- or Super-Critical Lane-Emden Systems with Neumann Boundary Conditions

Abstract

We prove that, for some suitable smooth bounded domain, there exists a solution to the following Neumann problem for the Lane-Emden system:

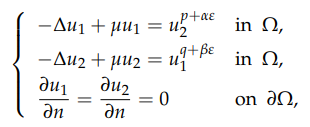
where $Ω$ is some smooth bounded domain in $\mathbb{R}^N,$ $N ≥ 4,$ $\mu > 0,$ $α > 0,$ $β > 0$ are constants and $ε\ne 0$ is a small number. We show that there exists a solution to the slightly supercritical problem for $ε > 0,$ and for $ε < 0,$ there also exists a solution to the slightly subcritical problem if the domain is not convex.
Comparing with the single elliptic equations, the challenges and novelty are manifested in the construction of good approximate solutions characterizing the boundary behavior under Neumann boundary conditions, in which process, the selection of the range of nonlinear coupling exponents and the weighted Sobolev spaces requires elaborate discussion.